Project #tweetprop: On Slabs versus Beams

The first proposition of my dissertation is the following:

The two-dimenional shear-carrying behaviour of one-way slabs under concentrated loads close to supports should be treated differently than the one-dimensional shear-caryring behaviour of beams.

or in Dutch (as the propositions are in English and Dutch:

Het tweedimensionale afschuifdraagvermogen van in één richting dragende platen onder geconcentreerde belastingen nabij de opleggingen moet anders behandeld worden dan het eendimensionale afschuifdraagvermogen van balken.

This proposition is one of the main findings of my research, and a conclusions that I have previously published in the ACI Structural Journal as well as in a number of conference papers.

Let me break the justification of this proposition down into the observations, and the explanations based on the experimental evidence as well as theoretical reasons.

What did we observe?

In our shear experiments, we subjected slabs to a concentrated load close to the support. We studied the influence of different parameters on the shear capacity. Most shear experiments in the literature are experiments on beams, that typically have a small cross-section, that are heavily reinforced in bending and that are tested in four-point bending. Our understanding of how different parameters effect the shear capacity is thus mostly supported by these experiments. When we compared our experiments to the knowledge from beams, we found differences. The shear capacity of slabs depends mostly on geometric parameters. In beam shear experiments, the capacity depends strongly on the concrete compressive strength. For the range of concrete strengths that we tested, we did not see such a strong dependence.

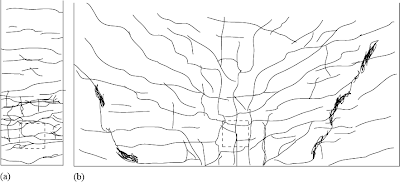
To study how the behavior changes from beam to slab, we tested a series of specimens with an increasing width. We found how the dependence of the shear capacity on parameters changes as the specimen width changes. We also saw how different the cracking pattern is for slabs as compared to beams.

In this figure, we see the bottom face after an experiment of a specimen of 0,5m wide and a specimen of 2,5m wide. All other parameters are kept identical. The “beam” specimen only has horizontal cracks, while the “slab” specimen has a grid-like pattern of horizontal and vertical cracks following the rebar, but also has inclined cracks on the bottom that indicate shear distress, and even some punching damage.

How can we explain this?

Let’s talk strut-and-tie models here. If we have a beam with a load close to the support, the load is carried by a compression strut between the load and the support – that’s in the Eurocode as well.
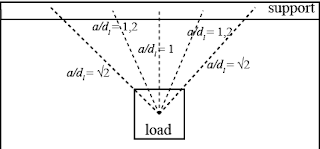
But what happens when we apply this to a slab? If we have a concentrated load, we know that the forces can “fan out” in the width direction.

This figure shows why the influence of the distance between the load and the support is different for slabs as compared to beams. We see the top view of a slab subjected to a concentrated load. In a beam, our compression strut is the line of a/dl = 1 from the figure. In a slab, we have many struts that can develop – an entire fan of them. So, we can say that in a slab, we develop a three-dimensional strut-an-tie model. Now, two dimensions play a role in our shear capacity: the distance between the load and the support (a or av), and the width of the specimen. If we then apply this idea to the effect of the distance between the load and the support to the shear capacity, we see that we need to account for a sort of “average distance” for all these struts in a slab (a/dl > 1 on average), while for a beam this is defined only by a/dl = 1.

To conclude: we saw in our experiments a difference between slabs and beams in their dependency on parameters to define the shear capacity. This difference can be explained by acknowledging that slabs carry concentrated loads in what can be represented by a three-dimensional strut-and-tie model. As such, slabs have a two-dimensional load-carrying behavior, which is different from the one-dimensional load-carrying behavior in shear that we know from beams (and that is well-documented in the literature).